摘要: 以DF77 叶片为原型, 通过改变叶片的预弯曲线, 分别得到预弯1.35 m、无预弯、预弯-1.35 m 3 种叶片模型。通过CFD 数值模拟3 种不同预弯叶片的流场, 分析叶片预弯程度对风电叶片气动性能和出力的影响。通过3 种方案结果分析表明, 无预弯的叶片功率最大。根据理论分析结果, 展望叶片预弯值的设计方法, 使叶片运行时达到最佳出力状态。
关键词: 风电叶片, 预弯, 气动性能, 数值计算
0 引言
风力发电机是将风能转换为电能的机械装置。叶片是风力发电机的主要部件, 其设计优劣直接决定了风力发电机组的发电效率。在风力机运行过程中, 由于风压的作用使得叶片发生弹性挠曲,LM 公司提出的叶片预弯设计方法能够简洁、经济地解决该问题[1]。叶片预弯能在来流风速变化时有效地调节风力发电机的输出功率。国内有关风力发电机叶片预弯方面的文献较少[2]。
转动叶片几何预弯的目的主要是避免运动干涉。具体来讲, 叶片迎风受力旋转所形成的旋转曲面形状往往会随风力载荷的变化而变化, 为了避免叶片与塔筒间的运动干涉, 在设计时把叶片进行了几何预弯处理。这样一方面可以降低叶片局部应力集中载荷; 另一方面, 刚度相对降低带来生产叶片原材料和工艺辅助材料的节省, 达到减轻叶片重量和降低成本的目的[3]。另外, 由于前倾预弯叶片可增大叶片与塔架之间的净空距离,在风轮旋转或强风时不会碰到塔架。结合风轮倾角和锥角的存在, 可缩短机组的主轴长度, 使风轮与机舱更加紧凑, 从而提高风机的稳定性[4]。在正常情况下, 叶片旋转时会弯向塔架, 弯曲后的叶片扫风面积变小, 发电量也随之减小, 而预弯设计可使叶片增大扫风面积, 提高发电量。
本文中并未考虑叶片是柔性的, 假设叶片为刚体来进行流场计算分析。通过对叶片的预弯曲线进行修改, 预弯从叶片根部开始, 最大预弯值分别为1.35 m, 0, -1.35 m。针对3 种预弯叶片模型进行数值模拟, 研究预弯对叶片气动性能及出力的影响。通过预弯数值计算分析, 提出一种设计预弯的方法。
1 模型及数值方法
1.1 几何模型
以DF77 叶片原型为基础, DF77 叶片长37.5m, 最大弦长3.183 m, 总扭角16°。适用于1.5MW 变速变桨风力发电机组, 最大功率系数0.48,叶片的几何外形如图1(a)所示。
为了分析预弯对叶片气动性能的影响, 将DF77 叶片预弯进行修改, 一种方案是原始叶片预弯值为1.35 m, 如图1(a)所示; 另一种方案DF77叶片取消预弯, 即为无预弯叶片, 如图1(b)所示;第三种方案将预弯改为-1.35 m, 即叶片朝塔架方向弯曲, 如图1(c)所示。

1.2 数值方法
CFD 数值模拟假设叶片为刚体不考虑叶片的变形[5]。CFD 数值模拟采用一方程湍流模型Spalart-Allmaras, 求解方法采用时间相关法求解雷诺平均NS 方程、中心节点的有限体积离散、显式龙格-库塔时间积分、全多重网格初场处理和多重网格迭代加速, 以及低速流动的预处理技术等。
1.3 网格介绍
三维叶片网格由AutoGrid5TM 自动生成: 在导入叶片几何、指定叶片数目与转速、指定计算域大小与网格分布后, 即可完成网格的自动生成和边界条件的自动设置。根据流动的周期性, 三叶片风力机计算域大小为120°圆柱, 如图2 所示。

计算网格总数约为290 万, 上下游各10 倍叶高, 径向6 倍叶高, 翼型弦向网格数161, 叶片展向网格数81。叶片表面绝大部分Y+均小于3。
1.4 边界条件
计算域外边界给定进出口边界条件: 来流侧给定速度分量和大气温度, 假定进口处具有相同的风速, 不考虑风速切变的影响, 进气方向为垂直进口面, 给出进口风速。其余计算域边界给定大气压力, 见图2。叶片壁面为无滑移边界, 轮毂采用欧拉边界[6——8]。
2 计算结果及分析
2.1 功率计算
1.5 MW 风力发电机组为变速变桨风机, 其运行曲线主要可以分为4 个区域(见图3): 最低转速区域(I 区): 风轮转速稳定在最小转速, 叶尖速比(TSR)随风速增大而减小, 功率系数Cp 在最大功率系数以下。最佳运行区域(II 区): 桨距角保持不变, 风轮转速随风速成正比增加, 机组运行在设计叶尖速比, Cp 保持最大值。次最佳运行区域(III 区): 转速达到额定值, 不再随风速增加, 桨距角仍然保持不变, 叶尖速比随风速增大而减小,Cp 开始下降。额定功率区域(IV 区): 转速和功率均维持在额定值, 桨距角随风速增大而增大, Cp降低。
根据上述变速变桨机组运行特性, 数值模拟上述3 种预弯叶片的气动性能。边界条件风速分别为5 m/s (最低转速区)、8 m/s (最佳运行区)、10.8 m/s(次最佳运行区)、15 m/s(额定功率区)和20 m/s(额定功率区)的情况, 计算出各个风速下对应的转矩(见表1), 根据式(1)计算出风轮的输出功率。
其中: P 为输出功率, kW; T 为风轮转矩,N·m; n 为风轮转速, r / min。
表1 给出了3 种不同预弯叶片在不同风速下数值计算得到的风轮转矩和功率, 可以看出, 随着风速增加, 3 只叶片的转矩和功率值呈增加的趋势, 但在20 m/s 的风速下却略显降低, 与叶片的桨距角20.3°过大有关, 从数值模拟的结果看, 该风速下桨距角应该适当降低, 使风轮吸收风能达到满发状态。另外, 从表1 中还可看出, 在相同风速下, 无预弯叶片的转矩和功率值最大。考虑到实际叶片的柔性特性, 在正常运行情况下, 叶片旋转时会弯向塔架, 无预弯的叶片弯曲后扫风面积变小, 发电量也随之减小(无预弯与预弯-1.35 m 对比结果); 而预弯叶片变形后可使叶片增大扫风面积, 提高发电量(预弯1.35 m 与无预弯对比结果)。

图4 给出不同预弯叶片情况下功率的对比结果, 从中可看出: 仅从叶片预弯方面考虑, 预弯值对风电机组的输出功率影响很大。以无预弯叶片功率值为基础, 当风速低于额定风速时, 预弯1.35 m 的叶片功率下降在0.5%内, 预弯-1.35 m的叶片比无预弯叶片功率降低3%左右; 当风速高于额定风速时, 预弯1.35 m 叶片功率下降1.8%左右, 预弯-1.35 m 叶片功率下降高达11%左右。由此可见, 在所研究的几个工况下, 无预弯叶片的功率始终大于预弯叶片, 随着风速的增加, 功率误差值逐渐增大, 见式(2)。

式中: γ 为相对误差, P0为无预弯叶片在各个风速下计算的功率。

为了鲜明对比, 选取2 个特征风速工况10.8m/s 和20 m/s 下的数值模拟结果作为研究对象,下面将对其进行定性和流场细节分析。
2.2 压力系数分布
以叶片展向20%、50%和80% 3 个截面翼型为主要研究对象, 对比分析3 种不同预弯叶片压力分布特性, 其中压力系数可通过式(3)求得。

其中: p 为翼型表面压力, Pa; p0为来流静压, Pa; ρ 为气体密度, 1.225 kg/m3, U∞为来流速度; ω 为风轮转速; r 为截面到轮毂中心的距离。根据式(3)计算得出不同风速下3 种预弯叶片各截面压力系数分布, 理论上讲, 叶片运行时存在攻角, 因此驻点一般在前缘压力侧, 此处速度为零, 压力最大, 沿压力侧向后缘移动, 速度先增大后减小, 压力先减小后增大, 压力系数先减小后增大; 驻点沿压力面向前缘及吸力侧后缘移动, 速度先增大后减小, 压力先减小后增大, 在吸力侧靠近前缘某处速度达到最大, 此时压力达到最大负压, 此处达到最大负压力系数值, 此后压力逐渐回升, 在后缘处接近压力侧压力值。
从图5 可以看出: 在相同风速下(10.8 m/s),越靠近叶尖, 截面翼型的压力差越大, 即靠近叶尖的翼型出力较大, 这一点与设计相符。对于特定风速特定截面, 可以看出, 不同预弯叶片截面翼型压力侧压力分布绝大部分重叠, 趋势一致,数值上只有微小的差别, 但是从吸力侧的压力分布曲线可以明显地看出, 无预弯的叶片截面吸力面的压力较低, 吸力峰值最大, 预弯1.35 m 叶片次之, 预弯-1.35 m 叶片压力最大, 因此无预弯叶片的压差较大, 使得无预弯的叶片功率较高。另外, 其他风速、各截面翼型计算结果同样满足这一趋势。
2.3 极限流线
叶片吸力侧的壁面极限流线可以反映分离点的位置, 图6 给出了10.8 m/s 风速下3 种不同预弯叶片的壁面极限流线图, 通过比较发现: 该风速下, 无预弯的叶片吸力面分离较晚, 预弯1.35m 叶片次之, 预弯-1.35 m 叶片吸力面分离提前,分离区域较大, 这也是预弯叶片引起功率降低的主要原因。同时叶片的壁面极限流线还反映了叶片三维边界层的影响: 分离区内二次流动在离心力作用下向叶尖处倾斜, 而科氏力则使叶片产生一个附加的弦向压力梯度, 使叶片边界层中的气流向后缘处流动并发生失速延迟。
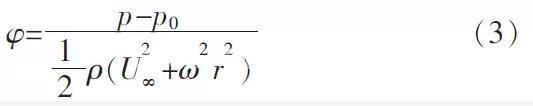
3 结论与展望
3.1 结论
采用CFD 软件对预弯1.35 m、无预弯和预弯-1.35 m 的3 种叶片在不同的风速条件下进行三维定常数值模拟。通过数值计算对比不同状态下风轮转矩结果, 并通过理论计算得到风轮功率,同时分析不同来流风速条件下的叶片三维流场,结果表明:
(1)从叶片预弯方面考虑, 无预弯叶片的功率始终大于预弯叶片, 在相同风速下, 无预弯叶片的转矩和功率最大, 随着风速的增加, 功率误差值逐渐增大。当风速低于额定风速时, 预弯1.35m 和预弯-1.35 m 叶片功率分别比无预弯降低0.5%和3%左右; 当风速高于额定风速时, 预弯1.35 m 和预弯-1.35 m 叶片功率分别比无预弯降低1.8%和11%左右。;
(2)考虑到叶片刚度和柔性特点, 在机组正常运行时, 叶片受到轴向推力作用而变形。无预弯的叶片变形后扫风面积变小, 发电量随之减小;而预弯叶片变形后可使叶片扫风面积增大, 提高发电量。因此, 叶片设计时需要选取合理的预弯值, 尽量使叶片弯曲后变为直叶片, 以达到扫风面积增大的情况, 但如果叶片弯曲变形过大, 则发电量将迅速降低。
(3)目前风电大功率机组均为变桨型, 机组承受的推力在额定风速时达到最大, 此时叶片面外的变形量也最大, 所以叶片预弯设计时需要综合考虑变形和刚度的问题, 保证叶片正常发电时处于比较直的位置, 提供额定风速前的风能吸收,达到提高发电量的目的。
3.2 展望
根据叶片预弯程度对出力性能的影响, 可归纳出预弯对机组设计有两方面好处。一方面可以增加叶片尖部与塔筒之间的净空距离, 保证机组运行时不会与塔筒干涉; 另外一方面预弯叶片运行时可以增加风轮的扫风面积, 随着叶片长度的增加柔性也越来越大, 如果叶片设计成预弯的话,机组运行起来叶片变形促使叶片长度增加。根据叶片设计适用风区的情况, 设计叶片预弯量的大小, 保证叶片在额定风速前的出力性能最好。叶片预弯可根据悬臂梁理论和每个风速下的轴向推力, 再结合叶片的一阶挥舞模态变形进行设计, 保证叶片最大变形后叶片处于比较直的位置。风力机叶片承受分布式轴向推力载荷作用,分布载荷可以看作由作用在各叶素段上的载荷所, 因此, 在该载荷作用下, 计算叶片的变形来设计叶片预弯程度。根据悬臂梁理论, 叶根r处的叶素段在轴向推力作用下, 叶片自由端挠度为:
式中: dT 为作用在叶素段上的轴向推力, N;R 为叶片半径, m; r 为当地半径, m; EI 为弯曲刚度, Nm2;
图7 给出了叶片的预弯变形情况, 通过式(4)计算叶片的变形量, 计算过程大致分为以下几步:
(1)根据叶片初步模型, 使用Bladed 软件计算正常发电工况下各风速下轴向推力情况;
(2)根据式(4)计算各风速轴向推力下的变形情况;
(3)结合步骤(2)的计算结果调整叶片各截面的刚度和变形情况, 保证叶片运行风轮扫风面积是最大的;
(4)重复以上步骤, 保证叶片在设计风区下,额定风速前正常运行时变形成直叶片。通过数值计算和理论分析, 用反向分析方法对叶片的预弯值进行设计, 总体思想是提高叶片的出力性能, 以此提供一种叶片预弯的设计方法。
作者:尹景勋, 李杰
东方电气风电有限公司




